
Ing. Axel Segura Richmond
Miembro CIT

Ing. Priscilla Meléndez Navarro
Miembro CIT

Ing. Wendy Gutiérrez Rodríguez
Miembro CIT
Resumen
En la determinación de las coordenadas ajustadas para un punto inaccesible, se estableció una red de apoyo horizontal medida con metodologías convencionales, aplicando dos variantes de observaciones angulares: ángulos y direcciones, así como distancias, cuya definición fue el resultado de un proceso de simulación con el programa Ajuste de Redes Geodésicas (ARGE). En la medición, se consideraron tres series completas. La configuración de la red contempló 16 ángulos, 18 direcciones y 6 distancias. El proceso de ajuste libre se realizó en dos partes, primero se consideraron ángulos y distancias, lo cual dio como resultado una desviación estándar a posteriori global de s0 = ± 1,033; y un segundo proceso de ajuste que consideró direcciones y distancias, donde la desviación estándar a priori global fue de s0 = ± 1,016. Se presenta a continuación una comparación de los principales parámetros derivados de los dos procesos de ajuste libre total, los cuales permitieron lograr una mejor exactitud global en la red de apoyo.
Introducción
El desarrollo del proyecto corresponde a la última evaluación del curso Ajuste II de la carrera de Ingeniería en Topografía y Geodesia, de la Escuela de Topografía, Catastro y Geodesia (ETCG) de la Universidad Nacional (UNA). El profesor del curso brindó las principales características del proyecto, entre las cuales se debía dar coordenadas a un punto inaccesible con una exactitud máxima de ± 3 mm y medirse con métodos convencionales, haciendo observaciones lineales y dos tipos de angulares. Para cumplir con el objetivo, preliminarmente se diseñó una red de control con base en la inspección de campo y tomando en consideración aspectos como la metodología, intervisibilidad entre los puntos y equipo disponible. Este diseño fue sometido a un proceso de simulación en el cual se realizaron una serie de adecuaciones para cumplir con los objetivos indicados.
Con base en los resultados de la simulación, se establecieron cinco vértices con visual al punto inaccesible (parte superior de una antena) ubicado sobre el edificio del Teatro Atahualpa del Cioppo, en el campus Omar Dengo, de la Universidad Nacional, por lo cual no era posible medir directamente en el punto. En campo se ejecutaron mediciones convencionales; en la primera etapa se realizaron observaciones de ángulos y distancias utilizando la estación total Topcon modelo GTS-235W, cuya exactitud angular es de ± 5” y lineal de ± 2 mm ± 2 ppm. Mientras que, en la segunda campaña de medición, se tomaron direcciones con la estación Topcon modelo GTS-236W, cuya presión angular es de ±6” y lineal de ± 2 mm ± 2 ppm.
Marco teórico
El ajuste geodésico por mediatas es un modelo conocido como Gauss-Markov, el cual se utiliza comúnmente cuando se requiere determinar una magnitud y no se puede extraer con métodos de medición directa, por ejemplo, las coordenadas de un punto inaccesible. Las coordenadas desconocidas se denominan incógnitas, mientras que a las magnitudes medidas a partir de ángulos, direcciones, distancias y azimut, entre otras, se les conoce como observaciones (Hidalgo Jiménez y Carrillo Quirós, 2011). Para que este tipo de ajuste por mediatas sea aplicable, es necesario contar con más observaciones que incógnitas (Rojas Porras, 2008), a fin de lograr resolver el problema geométrico, aplicar de forma correcta el ajuste y obtener valores ajustados de calidad. Además, con la aplicación del método, es posible determinar el grado de confiabilidad del trabajo y, por ende, definir si se puede utilizar o no (Araque Skinner, 2013).
Dentro del ajuste, se pueden considerar dos tipos: el ajuste amarrado, que contempla un vínculo de la red a una serie de puntos fijos conocidos, de los cuales se tienen sus coordenadas, para que la red intente acomodar la forma tanto a los puntos fijos como a los puntos nuevos, tomando como prioridad los puntos fijos (Valverde Calderón y Ramírez Núñez, 2023). Por otra parte, el ajuste libre define la geometría de la red por las observaciones, lo cual hará que la forma no se vea afectada, es decir, en todo momento tendrá la misma forma (Sevilla, 2005). Para considerar una red como libre, se deben tomar en cuenta diferentes factores, como que en la red no haya determinado un punto de origen para fijar el sistema de referencia, lo que daría lugar a una indeterminación en traslación (posición, un parámetro libre en redes altimétricas, dos parámetros en redes planimétricas y tres en redes tridimensionales); o también podría existir una indeterminación de la rotación (orientación, con la misma cantidad de parámetros que en el caso de la traslación), lo que sucede cuando hay inexistencia de ángulos de orientación en la red o una indeterminación en la escala (un parámetro por igual para los tres tipos de redes), en caso de que no se hayan obtenido distancias sobre ninguna línea de la red (Sevilla, 2005).
La funcionalidad de las incógnitas de orientación es vincular la dirección observada con el azimut, por lo que se necesita un azimut aproximado y una dirección. Teniendo así la siguiente función:

Donde se tiene que:
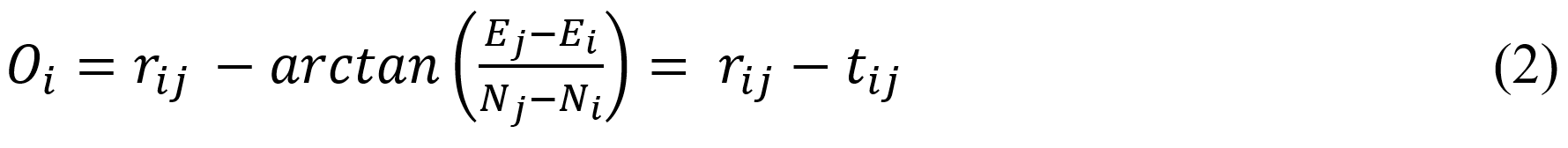
Donde,
O: incógnita de orientación
r: dirección medida
t: azimut
La solución del ajuste está basada en el principio de mínimos cuadrados, el cual establece que “la suma de los cuadrados de los errores residuales debe ser mínima” (Sevilla, 1987, p.104) y se describe a partir de la métrica euclídea como:

la cual, si está definida a partir de las observaciones de la matriz P, se describe matricialmente como:

El principio antes mencionado parte del modelo matemático, el cual considera el modelo funcional y el modelo estocástico. El modelo funcional hace referencia a la relación matemática entre los parámetros (incógnitas) y las observaciones fundamentadas en las propiedades geométricas o físicas del problema (Sevilla, 1986). Entonces, matemáticamente este modelo funcional considera las incógnitas X; las observaciones medidas LT; y los grados de libertad, los cuales son calculados de la siguiente forma:

Donde,
n: número de observaciones
u: número de incógnitas
d: defecto de datum
El defecto de datum está dado por aquellos parámetros faltantes para enlazar la configuración de la red en el sistema coordenado y que, para el caso de una red bidimensional, serían dos traslaciones y una rotación, siendo el defecto de datum igual a tres (Roldán, 1988).
Además, este modelo describe la relación entre las observaciones y las incógnitas a través de una función, la cual usualmente no se encuentra linealizada L=Φ (x) (siendo esta última función la definición del modelo funcional). Dentro de este modelo, se consideran pequeñas correcciones denominadas residuos (v), y se muestran como resultado los valores de las incógnitas, pero ajustados (Rojas Porras, 2008).
Ahora bien, el modelo estocástico está relacionado con la exactitud de las magnitudes encontradas durante la aplicación del modelo funcional, la cual depende de las observaciones. Este modelo está dado por la matriz de varianza-covarianza ll=02Qll, la cual posee en su diagonal los pesos de las observaciones. Usualmente, las estimaciones se determinan a partir del fabricante del equipo utilizado durante la medición, o a partir del conocimiento y experiencia individual (Rojas Porras, 2008). Parte importante de la aplicación adecuada de este modelo es que la estimación correcta de los pesos permite realizar la corrección que se les debe aplicar a las observaciones durante el ajuste (Ghilani y Wolf, 2006).
Considerando lo anterior, al realizar un ajuste en la estimación, es necesario considerar la aplicación del equilibrio de varianzas para mejorar el resultado obtenido; sin embargo, se sabe que, al usar este concepto en el ajuste, se modificará la varianza de referencia inicial para lograr que el modelo matemático sea aceptado con el 95 % de probabilidad. A pesar de esto, se debe tomar en cuenta que modificar la varianza inicial provocará que la calidad en los resultados obtenidos disminuya (Moya, 2022).
En la aceptabilidad de los datos, a todo ajuste topográfico se le aplica y se trabaja con un test estadístico con un 95 % de confianza; este porcentaje es el límite teórico dentro del cual debería estar el 95 % de los errores del grupo de observaciones. Este valor de error probable es común en topografía, para expresar la precisión y verificar la existencia de valores atípicos dentro de los datos (Ghilani y Wolf, 2006).
En el caso del programa utilizado (ARGE), se aplica el test global a la desviación estándar a priori s0 para calcular los intervalos de confianza (el límite inferior y el límite superior) de la desviación estándar teórica o a priori 𝝈0, el cual debe encontrarse dentro de dichos intervalos para que la prueba de la varianza se acepte (Dörries y Gonzáles, 2001).
Metodología
En la primera etapa del proyecto se realizó una visita de campo guiada por el profesor, donde se indicó el área en la cual se debía desarrollar la red y, tras un análisis, se determinó la ubicación de cinco vértices alrededor del punto inaccesible; desde cada uno de ellos había visual hacia P5 y en la mayoría de estos había intervisibilidad. Con base en la información obtenida, se realizó una simulación de la red en el programa ARGE, tomando en cuenta las observaciones que se presentan en las figuras 1 y 2.
Figura 1.
Diseño preliminar de la red con ángulos y distancias
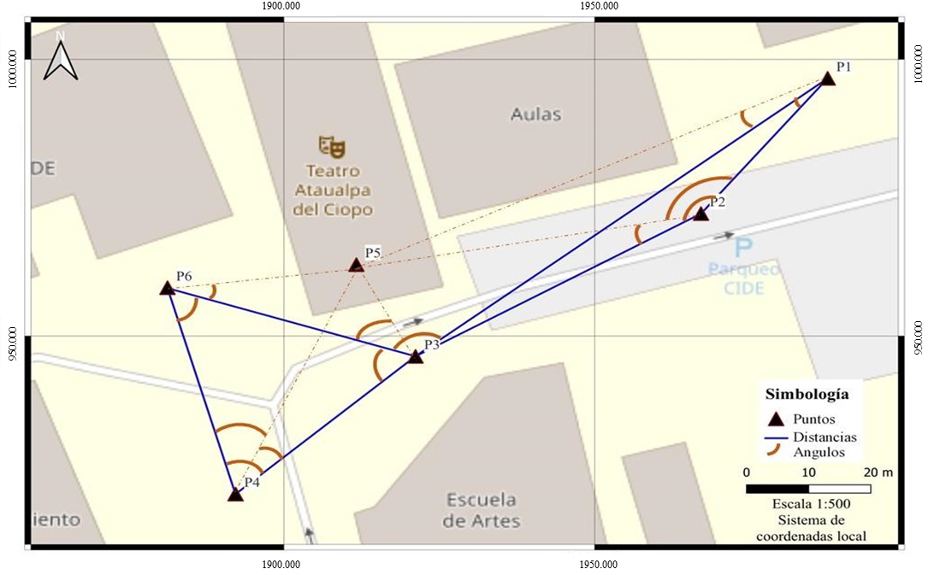
Fuente: Elaboración propia.
En la figura 1 se muestra el diseño de red preliminar con los puntos planteados, así como las observaciones lineales en color azul y los ángulos en color naranja.
Figura 2.
Diseño preliminar de la red con direcciones
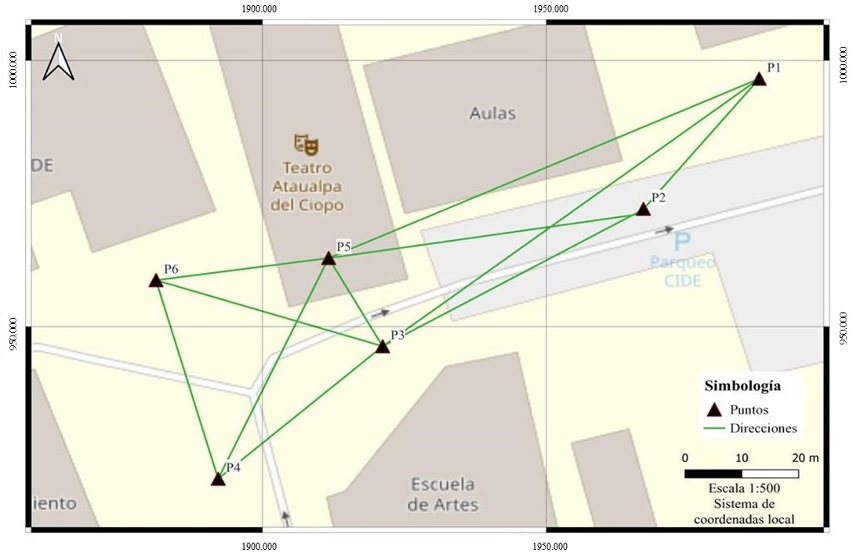
Fuente: Elaboración propia.
En la figura 2 se representan gráficamente los puntos y las direcciones tomadas en cuenta en la simulación de la red. Dado que los resultados obtenidos cumplían con la tolerancia establecida para el proyecto, se utilizaron como base para las mediciones.
Figura 3.
Fotografía de la antena (P5)

Fuente: Elaboración propia.
En la figura 3 se observa el objetivo del proyecto. Es una antena de forma circular posicionada en la cúspide de una estructura metálica saliente del techo de una edificación utilizada como teatro. A este elemento de telecomunicación, su ubicación y altura lo hacen inaccesible para poder estacionar sobre él.
En la primera campaña de medición se observaron ángulos y distancias, por lo cual se colocó la estación sobre el punto P2 y se utilizaron dos prismas sobre trípodes centrados en los puntos P3 y P1. Se inició la observación en posición I del instrumento, se visó P3, se fijó la lectura en 0° en el limbo horizontal, luego se abrió el tornillo de fijación y se generó el ángulo hacia la derecha. Aún en posición I, se hizo la lectura hacia P1 y se anotó en la libreta de campo tanto el ángulo como la distancia. Posteriormente, se dio vuelta campana al anteojo y se giró la alidada en 180°. Cuando el instrumento estuvo en posición II, se visualizó el punto P1 y luego se giró hacia P3; el procedimiento se repitió hasta tener tres series completas en todos los puntos.
En la segunda campaña, se midieron direcciones; se posicionó la estación total sobre P1 y se visó el prisma sobre el punto P2. Cabe mencionar que el 0° del instrumento ocupó una posición arbitraria, no se fijó como en la medición de ángulos. Se hizo la lectura en la posición I y se anotó en la libreta de campo; luego se hizo vuelta campana y se giró la alidada para medir en posición II. Este proceso se realizó hasta tener dos series completas en todos los vértices de la red.
Tomando las observaciones obtenidas en campo, se hizo un promedio por serie en cada estación y se prepararon para su debido ajuste en el programa ARGE DOGO. En el cálculo de las coordenadas aproximadas, se utilizó un sistema local iniciando en P1 con coordenadas 2000 m en la componente Este y 1000 m en la Norte, y se calcularon las restantes de los puntos de red mediante el dibujo de los ángulos y distancias medidas en campo, usando el programa Civil 3D de Autodesk; además, se utilizó el método de dibujar círculos con radios iguales a la distancia, tal y como lo enseñó el profesor.
Cuadro 1.
Coordenadas aproximadas
| Punto | Este (m) | Norte (m) |
| P1 | 2000,000 | 1000,000 |
| P2 | 2007,860 | 1026,890 |
| P3 | 1947,200 | 925,220 |
| P4 | 1923,370 | 956,520 |
| P5 | 1945,130 | 977,520 |
| P6 | 1970,740 | 953,580 |
Fuente: Elaboración propia.
Haciendo uso de las computadoras disponibles en el laboratorio, se crearon dos proyectos en ARGE: en el primer proceso de ajuste libre para ángulos y distancias incluyendo 12 incógnitas y 19 observaciones, se identificaron y excluyen las observaciones groseras; en el segundo procedimiento se ingresaron 18 direcciones y 6 distancias para el ajuste libre, se detectó una observación grosera y fue excluida del proceso, se realizó una iteración y se obtuvieron las coordenadas ajustadas. Durante el proceso de ajuste, se contó con la guía y recomendaciones del profesor del curso Dr. Ing. Jorge Moya Zamora.
Resultados y análisis
A continuación, se detallan los datos recolectados en campo. En la primera columna se muestra la estación ocupada (i); en la segunda, la puntería izquierda (j); y en la columna tres, la puntería derecha (k). Además, la cuarta columna contiene las mediciones en unidades centesimales.
Cuadro 2.
Observaciones de ángulos
| i | j | k | Ángulos (gon) |
| P2 | P1 | P6 | 11,9051 |
| P2 | P6 | P5 | 27,7090 |
| P1 | P5 | P2 | 142,5290 |
| P1 | P3 | P5 | 36,1056 |
| P1 | P6 | P3 | 39,4703 |
| P6 | P2 | P1 | 6,0544 |
| P6 | P5 | P2 | 81,6296 |
| P6 | P3 | P5 | 103,9330 |
| P3 | P4 | P5 | 39,0149 |
| P3 | P5 | P1 | 41,4907 |
| P3 | P1 | P6 | 5,0094 |
| P4 | P5 | P6 | 52,7509 |
| P4 | P6 | P3 | 54,6184 |
Fuente: Elaboración propia.
En el cuadro 3, se colocaron las observaciones de las direcciones. En la columna uno se presentan las estaciones ocupadas (i); y en la segunda, el punto observado (j); y en la tercera, el promedio por serie de las direcciones en gones.
Cuadro 3.
Observaciones de direcciones
| i | j | Dirección (gon) |
| P2 | P1 | 379,4830 |
| P2 | P6 | 391,3800 |
| P2 | P5 | 19,0943 |
| P1 | P6 | 35,9756 |
| P1 | P3 | 39,3414 |
| P1 | P5 | 75,4514 |
| P1 | P2 | 218,0208 |
| P6 | P1 | 78,0686 |
| P6 | P2 | 72,0147 |
| P6 | P5 | 390,3874 |
| P6 | P4 | 346,3030 |
| P6 | P3 | 286,4438 |
| P3 | P4 | 48,1617 |
| P3 | P5 | 87,1750 |
| P3 | P1 | 128,6650 |
| P3 | P6 | 133,6727 |
| P4 | P5 | 64,4090 |
| P4 | P6 | 117,1590 |
| P4 | P3 | 172,5049 |
Fuente: Elaboración propia.
Las distancias medidas en campo se muestran en el cuadro 4; estas son el promedio de las tres series anotadas en la libreta.
Cuadro 4.
Observaciones de distancias
| i | j | Distancia (m) |
| P2 | P1 | 28,0151 |
| P2 | P6 | 82,1739 |
| P1 | P6 | 54,8745 |
| P1 | P3 | 91,5421 |
| P4 | P6 | 47,4615 |
| P3 | P6 | 36,8545 |
| P3 | P4 | 39,3485 |
Fuente: Elaboración propia.
Con las observaciones de ángulos y distancias, el ajuste de minimización total de traza se obtuvo una desviación estándar a posteriori global de s0 = 1,033, con 12 incógnitas, 19 observaciones y 10 grados de libertad. Según los resultados y al 95 % de probabilidad, el ajuste se acepta (cuadro 5).
Cuadro 5.
Resumen de los resultados del ajuste obtenidos mediante observaciones de ángulos y distancias
| Gr | Observación | Nombre | σ0 | s0 | vTPv | Redun. |
| 1 | Ángulos | TOPCON W235 | ± 28,00 cc | 1,02 | 8,14 | 7,77 |
| 1 | Distancias | TOPCON W235 | 2 mm ± 2 ppm | 1,06 | 2,53 | 2,23 |
Fuente: Elaboración propia.
La desviación estándar a priori para los ángulos en el primer proceso se estableció en ±15 cc. Sin embargo, se hizo un equilibrio de varianzas con las mismas observaciones, pero con el peso en ±28 cc, resultado que evidencia un adecuado modelo estocástico inicial, por lo que el ajuste se acepta. Además, con base en la redundancia grupal, se determina que las observaciones angulares tienen mayor aporte que las distancias en el ajuste.
Cuadro 6.
Coordenadas ajustadas a partir de ángulos y distancias
| Punto | T | Aprox. E (m) | Aprox. N (m) | Delta E (m) | Delta N (m) | Ajust. E (m) | Ajust. N (m) | Sigma E (mm) | Sigma N (mm) |
| P1 | D | 2000,003 | 999,962 | 2,4 | -0,4 | 2000,005 | 999,961 | 0,7 | 0,9 |
| P2 | D | 2007,761 | 1026,902 | -1,2 | 0,8 | 2007,760 | 1026,903 | 1,0 | 1,2 |
| P3 | D | 1947,165 | 925,209 | -0,3 | 2,2 | 1947,165 | 925,211 | 0,7 | 0,8 |
| P4 | D | 1923,374 | 956,552 | -0,5 | 0,6 | 1923,374 | 956,552 | 0,9 | 1,4 |
| P5 | D | 1945,257 | 977,566 | -1,3 | -2,4 | 1945,256 | 977,563 | 1,0 | 1,0 |
| P6 | D | 1970,740 | 953,540 | 0,9 | -0,7 | 1970,741 | 953,540 | 0,6 | 0,7 |
Fuente: Salida del programa ARGE-DOGO.
Cuadro 7.
Observaciones de ángulos y distancias ajustadas
| Tipo | Grupo | Estación | Hacia | Med / Ajust (gones / m) | l / p (mm) | v/s (mm) | r/n |
| ANG | 01 | P1 | P3
P5 |
36,10563
36,10522 |
-26,6
0,0 |
-4,1
14,0 |
0,8
4,0 |
| ANG | 01 | P1 | P5
P2 |
142,56117
142,56425 |
-111,1
0,0 |
30,8
23,1 |
1,5
0,8 |
| ANG | 01 | P1 | P6
P5 |
39,47034
39,47025 |
-16,6
0,0 |
-0,9
14,0 |
0,8
4,0 |
| ANG | 01 | P2 | P1
P6 |
11,90514
11,90811 |
35,8
0,0 |
29,7
17,0 |
0,7
2,7 |
| ANG | 01 | P2 | P6
P5 |
27,70903
27,70855 |
5,0
0,0 |
-4,8
10,5 |
0,9
7,1 |
| ANG | 01 | P3 | P4
P5 |
39,01487
39,01518 |
1,1
0,0 |
3,1
22,6 |
0,4
1,5 |
| ANG | 01 | P3 | P5
P1 |
41,49069
41,49418 |
5,4
0,0 |
34,9
16,6 |
0,7
2,9 |
| ANG | 01 | P3 | P1
P6 |
5,00941
5,01322 |
-15,5
0,0 |
38,1
17,2 |
0,6
2,7 |
| ANG | 01 | P4 | P5
P6 |
52,75090
52,75145 |
-23,8
0,0 |
5,5
21,9 |
0,4
1,6 |
| ANG | 01 | P4 | P6
P3 |
54,61842
54,62051 |
-55,6
0,0 |
20,9
18,3 |
0,6
2,3 |
| ANG | 01 | P6 | P2
P1 |
6,05437
6,05739 |
2,1
0,0 |
30,2
9,2 |
0,9
9,3 |
| ANG | 01 | P6 | P5
P2 |
81,62958
81,62927 |
34,7
0,0 |
-3,1
22,2 |
0,4
1,6 |
| ANG | 01 | P6 | P3
P5 |
103,93300
103,93508 |
-120,6
0,0 |
20,8
24,0 |
0,3
1,4 |
| DIS | 01 | P1 | P6 | 54,878
54,876 |
0,1
0,4 |
0,9
1,1 |
0,5
1,7 |
| DIS | 01 | P1 | P3 | 91,542
91,540 |
0,9
0,4 |
-1,6
1,2 |
0,4
1,6 |
| DIS | 01 | P2 | P6 | 82,174
82,174 |
0,4
0,4 |
-0,1
1,5 |
0,0
1,0 |
| DIS | 01 | P3 | P6 | 36,854
36,855 |
-2,8
0,4 |
1,4
1,0 |
0,6
2,2 |
| DIS | 01 | P3 | P4 | 39,348
39,348 |
-1,5
0,4 |
0,4
1,3 |
0,3
1,3 |
| DIS | 01 | P4 | P6 | 47,462
47,463 |
0,9
0,4 |
0,6
1,1 |
0,5
1,8 |
Fuente: Salida del programa ARGE-DOGO.
Cuadro 8.
Resumen de los resultados del ajuste obtenidos mediante observaciones de direcciones y distancias
| Gr | Observación | Nombre | σ0 | s0 | vtPv | Redun, |
| 1 | Direcciones | TOPCON W236 | ± 25,00 cc | 0,98 | 7,29 | 7,60 |
| 1 | Distancias | TOPCON W235 | 2 mm ± 2 ppm | 1,13 | 3,04 | 2,40 |
Fuente: Elaboración propia.
En el ajuste que consideró las direcciones y distancias, se obtuvo una red con 24 observaciones, 12 incógnitas y 10 grados de libertad, lo cual dio como resultado una varianza global de s0 = 1,016. La desviación estándar a priori para las distancias se dejó de acuerdo con las especificaciones del fabricante del equipo, y para las direcciones se modificó, ya que el primer error utilizado fue de ± 18 cc y se aumentó a ± 25 cc, modelo que fue más acertado de acuerdo con los resultados. La redundancia de las direcciones es mayor que la de distancias, y su varianza a posterior se acerca más a la unidad.
Cuadro 9.
Coordenadas ajustadas a partir de direcciones y distancias
| Punto | T | Aprox. E (m) | Aprox. N (m) | Delta E (m) | Delta N (m) | Ajust. E (m) | Ajust. N (m) | Sigma E (mm) | Sigma N (mm) |
| P1 | D | 2000,003 | 999,962 | 0,0 | 0,0 | 2000,003 | 999,962 | 0,8 | 1,1 |
| P2 | D | 2007,761 | 1026,902 | 0,0 | -0,0 | 2007,761 | 1026,902 | 1,0 | 1,5 |
| P3 | D | 1947,165 | 925,209 | 0,0 | 0,0 | 1947,165 | 925,209 | 1,0 | 1,0 |
| P4 | D | 1923,374 | 956,552 | 0,0 | -0,0 | 1923,374 | 956,552 | 1,1 | 1,1 |
| P5 | D | 1945,257 | 977,566 | -0,0 | 0,0 | 1945,257 | 977,566 | 1,2 | 1,2 |
| P6 | D | 1970,740 | 953,540 | -0,0 | -0,0 | 1970,740 | 953,540 | 0,7 | 0,7 |
Fuente: Salida del programa ARGE-DOGO.
En el cuadro 9, se presentan las coordenadas ajustadas a partir del ajuste con direcciones y distancias; se observa que, en la columna de los deltas, los valores son iguales a cero, debido a que se realizó el proceso de una iteración, tomando las coordenadas ajustadas como aproximadas y volviendo a ajustar, a fin de asegurar mínimos errores para obtener los valores resultantes.
Cuadro 10.
Observaciones de direcciones y distancias ajustadas
| Tipo | Grupo | Estación | Hacia | Med / Ajust (gones / m) | l / p (mm) | v/s (mm) | r/n |
| DIR | 01 | P1 | P6 | 35,97562
35,97728 |
-16,6
0,0 |
16,6
10,2 |
0,6
6,0 |
| DIR | 01 | P1 | P3 | 39,34136
39,34099 |
3,7
0,0 |
-3,7
9,7 |
0,6
6,7 |
| DIR | 01 | P1 | P5 | 75,45139
75,44929 |
21,0
0,0 |
-21,0
13,3 |
0,5
3,6 |
| DIR | 01 | P1 | P2 | 218,02076
218,02157 |
-8,1
0,0 |
8,1
18,1 |
0,2
1,9 |
| DIR | 01 | P2 | P1 | 379,48302
379,48190 |
11,2
0,0 |
-11,2
11,7 |
0,5
4,6 |
| DIR | 01 | P2 | P6 | 391,38002
391,38345 |
-34,3
0,0 |
34,3
7,8 |
0,6
10,2 |
| DIR | 01 | P2 | P5 | 19,09429
19,09198 |
23,1
0,0 |
-23,1
9,8 |
0,5
6,5 |
| DIR | 01 | P3 | P4 | 48,16165
48,15971 |
19,4
0,0 |
-19,4
16,9 |
0,3
2,2 |
| DIR | 01 | P3 | P5 | 87,17500
87,14447 |
5,3
0,0 |
-5,3
12,5 |
0,5
4,0 |
| DIR | 01 | P3 | P1 | 128,66505
128,66462 |
4,3
0,0 |
-4,3
11,7 |
0,5
4,6 |
| DIR | 01 | P3 | P6 | 133,67269
133,67558 |
-28,9
0,0 |
28,9
12,5 |
0,5
4,0 |
| DIR | 01 | P4 | P5 | 64,40895
64,40731 |
16,4
0,0 |
-16,4
14,4 |
0,2
3,0 |
| DIR | 01 | P4 | P6 | 117,15895
117,16059 |
-16,4
0,0 |
16,4
14,4 |
0,2
3,0 |
| DIR | 01 | P6 | P1 | 78,06860
78,06847 |
1,3
0,0 |
-1,3
13,7 |
0,5
3,3 |
| DIR | 01 | P6 | P2 | 72,01466
72,01431 |
3,5
0,0 |
-3,5
12,8 |
0,5
3,8 |
| DIR | 01 | P6 | P5 | 390,38738
390,38820 |
-8,2
0,0 |
8,2
20,3 |
0,2
1,5 |
| DIR | 01 | P6 | P4 | 346,30301
346,30329 |
-2,8
0,0 |
2,8
17,0 |
0,4
2,2 |
| DIR | 01 | P6 | P3 | 286,44375
286,44314 |
6,1
0,0 |
-6,1
16,9 |
0,4
2,2 |
| DIS | 01 | P1 | P6 | 54,875
54,875 |
0,1
0,2 |
-0,1
1,5 |
0,4
1,7 |
| DIS | 01 | P1 | P3 | 91,542
91,541 |
0,9
0,2 |
-0,9
1,6 |
0,4
1,6 |
| DIS | 01 | P2 | P6 | 82,174
82,174 |
0,4
0,2 |
-0,4
2,0 |
0,1
1,0 |
| DIS | 01 | P3 | P6 | 36,854
36,857 |
-2,8
0,2 |
2,8
1,4 |
0,5
2,0 |
| DIS | 01 | P3 | P4 | 39,348
39,350 |
-1,5
0,2 |
1,5
1,5 |
0,5
1,8 |
| DIS | 01 | P4 | P6 | 47,462
47,461 |
0,9
0,2 |
-0,9
1,4 |
0,5
2,0 |
Fuente: Salida del programa ARGE-DOGO.
El resultado de las coordenadas planimétricas de los puntos debe ser considerado junto con su error (sigma), debido a que de ahí parte el hecho de las elipses absolutas de confianza al 95 % de confianza que se utiliza en redes bidimensionales; estas indican el gráfico de la región en donde se encuentran las coordenadas ajustadas. Lo ideal para las elipses es que sean lo más pequeñas y redondas posibles, a fin de garantizar mayor exactitud y mejor distribución de los errores con respecto al semieje mayor a, el semieje menor b y el ángulo de rotación q del semieje mayor.
Figura 4.
Comparación de elipses de confianza al 95 % de las dos variantes del ajuste
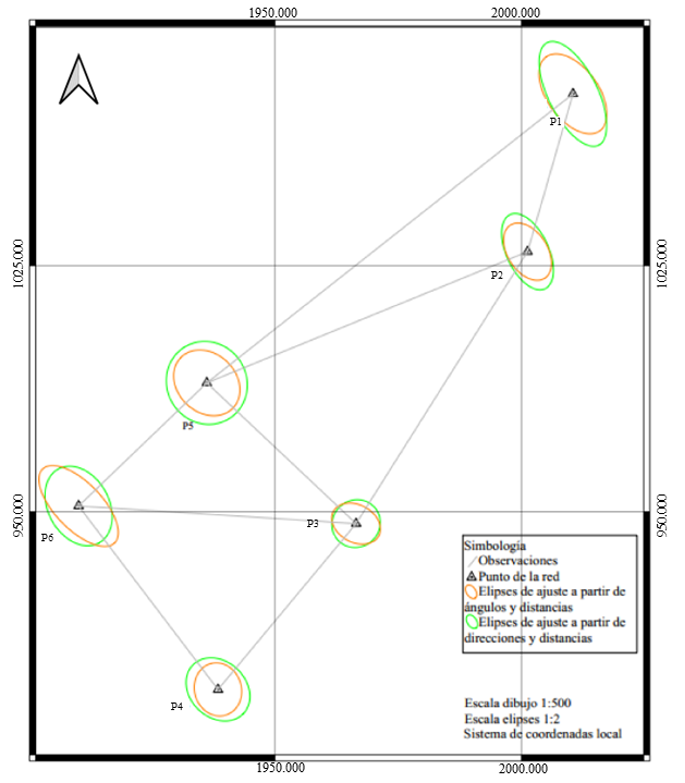
Fuente: Elaboración propia.
En la figura 4 se presentan las elipses de confianza obtenidas en los ajustes. Por las dimensiones de la elipse, el punto que presenta mayor precisión es el P4 y el de menor es el P2, dado que el tamaño de la elipse es proporcional a la desviación estándar del punto. En general, las elipses resultantes del ajuste de las direcciones y distancias son de mayor dimensión, ya que sus errores son mayores en las componentes Este y Norte. Cabe destacar que ambas metodologías cumplen con la tolerancia de ±3 mm establecida para el proyecto en las coordenadas Este y Norte, pero la metodología de ángulos y distancias brindó coordenadas con menos errores (figuras 5 y 6).
Figura 5.
Comparación de errores en las coordenadas de la componente Este
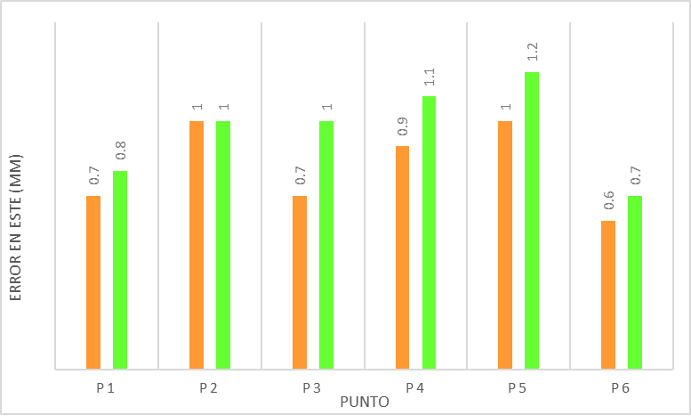
Fuente: Elaboración propia.
Figura 6.
Comparación de errores en las coordenadas de la componente Norte
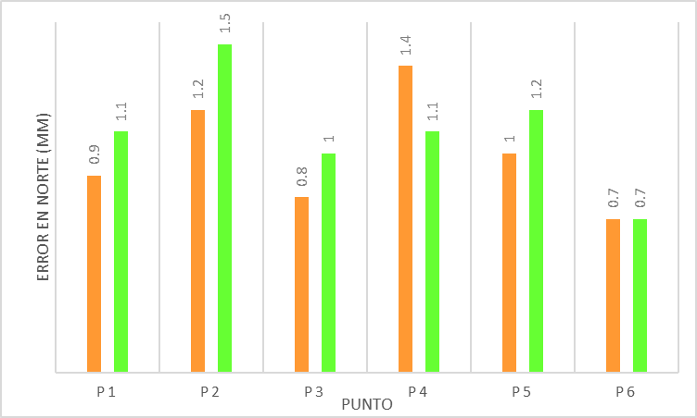
Fuente: Elaboración propia.
En ambas metodologías, la mayoría de los errores de las coordenadas planimétricas ajustadas de los puntos discrepan entre 0,1 mm y 0,1 mm; la mayor diferencia se da en las coordenadas Norte del punto P4, el cual tiene una discrepancia de 0,3 mm. El resultado de las coordenadas debe ser considerado junto con su error (s0), debido a que de ahí parte el hecho de las elipses absolutas de confianza que al 95 % de confianza, estas indican un gráfico de una región en donde se encuentra la coordenada ajustada de los puntos ―esto en redes bidimensionales―. Lo ideal para estas elipses es que sean lo más pequeñas y redondas posibles, para garantizar mayor exactitud y una mejor distribución de sus errores con respecto a cada semieje, respectivamente.
Conclusiones
- La técnica de equilibrio de varianza se emplea para reducir los errores de las mediciones angulares, lo cual contribuye a un ajuste de la red con mayor precisión en las desviaciones estándar globales, Por este motivo, se utilizó esta metodología para mejorar los errores a priori de las observaciones de ángulos y direcciones.
- Los resultados de las elipses absolutas de confianza demuestran que las dos metodologías utilizadas para medir la red y ajustar las coordenadas del punto inaccesible fueron muy precisas; sin embargo, en la metodología de ángulos, las elipses absolutas de confianza se comportan de una manera más equilibrada con respecto a los semiejes a, b y ɵ, con lo cual se representa una buena distribución en los errores de las coordenadas.
- Se puede afirmar que el estado físico de los equipos influye en gran medida en los resultados de las varianzas calculadas en el ajuste, por ende, para obtener resultados de mayor precisión, se deben usar equipos de buena calidad y en buen estado, para que no haya ruido en las observaciones obtenidas en el levantamiento, además de realizar series completas que permitan identificar errores groseros.
- Con los resultados obtenidos del proyecto, se logra identificar la importancia de utilizar el ajuste como herramienta fundamental para definir una mejor calidad de los datos a partir de una red prediseñada y, si fuera el caso, determinar si el error se encuentra en las coordenadas, en las observaciones o en los pesos de los errores del equipo utilizado,
Referencias
Araque Skinner, J. (2013). Elementos de pre-análisis de diseño de redes geodésicas para el control de obras civiles. Ingeniería, Revista de la Universidad de Costa Rica, 23(2), 65-73. https://revistas.ucr.ac.cr/index.php/ingenieria/article/view/8209/pdf_17
Dörries, E. y González, A. (2001). Manual: Ajuste de Redes Geodésicas DOGO.
Ghilani, C. D. y Wolf, P. R. (2006). Adjustment Computations: Spatial Data Analysis. https://www.academia.edu/33416657/Adjustment_Computation_Ghilani
Hidalgo Jiménez, R. J. y Carrillo Quirós J. M. (2011). Propuesta de densificación al tercer orden de la red geodésica nacional en la zona del levantamiento catastral de Istarú. [Proyecto de graduación]. Universidad de Costa Rica. http://eit.ucr.ac.cr/wp-content/uploads/2021/11/011_TFG_PD_HIDALGO_ET_AL_2011.pdf
Moya, J. (2022). Procesamiento GNSS en el marco geodésico CR-SIRGAS: Influencia de las épocas de observación y referencia. Ingeniería, Revista de la Universidad de Costa Rica, 32(2), 48-85. https://revistas.ucr.ac.cr/index.php/ingenieria/article/view/50181/51264
Rojas Porras, A. M. (2008). Medición y ajuste de una red tridimensional determinada con metodología convencional. [Tesis de grado]. Universidad Nacional de Costa Rica.
Roldán, J. (1988). Ajuste 2. Escuela de Topografía, Catastro y Geodesia. Universidad Nacional de Costa Rica, Heredia.
Sevilla, M. J. (1986). Formulación de modelos matemáticos en la compensación de redes geodésicas. III curso de geodesia superior. En Instituto de Astronomía y Geodesia, Cursos y Seminarios, 2, (pp. 2-69). Publicación núm. 148. https://digital.csic.es/handle/10261/25288
Sevilla, M. J. (1987). Colocación de mínimos cuadrados. En Instituto de Astronomía y Geodesia, IV Curso de Geodesia Superior: el problema de contorno de la geodesia física y estudio de deformaciones de la corteza, (pp. 97-141). Publicación núm. 157. http://hdl.handle.net/10261/25170
Sevilla, M. J. (2005). Ajuste de redes libres. Modelos matemáticos singulares. En Instituto de Astronomía y Geodesia, Curso de Doctorado. Publicación núm. 200. https://digital.csic.es/handle/10261/23397
Valverde Calderón, J. y Ramírez Núñez, M. (2022). Desarrollo de una herramienta informática para el ajuste de redes geodésicas en la carrera de Ingeniería en Topografía y Geodesia de la Universidad Nacional, Costa Rica. Revista Geográfica de América Central, 1(70), 135-152. https://doi.org/10.15359/rgac.70-1.5


